1. 서 론
최근 조류발생으로 인한 문제점이 발생함에 따라 정체수역의 수질관리에 대한 연구가 진행 되어왔다. 정체수역은 호소 및 유속이 낮은 구역에서 상하 유동이 발생하지 않아 혼합 구간이 적고 낮은 유속에 의해 오염물질의 축적이 가중되는 현상이 발생한다. 또한 상하 혼합구간이 적어 저층에 빈산소층이 발생하고 혐기화를 초례하여 수생태계의 직접적인 영향을 미치는 것으로 보고되고 있다[1~3].
이러한 문제점을 해결하기 위한 수단으로 중소 규모의 시설로 태양광 물순환장치, 대류식 교반장치 등이 개발되었다. 스크류 형태의 회전 Dish를 이용하여 유도관을 통해 저층수가 표층으로 상승하여 대기와 접촉 후 다시 하강하는 원리로 순환하는 시스템이다. 그러나 유량 및 토출 유속이 0.8 m/s 이하로 물순환이 가능한 영향범위가 작아 직접적인 수질 개선효과를 기대하기에는 어려움이 있다[4]. 또한 호소 및 해양에서 발생한 조류를 제거하기 위하여 새로운 개념으로 개발된 DCG (Density Current Generator)는 양흡식형 터빈식 프로펠러를 사용하여 저층수와 표층수를 흡입하고 혼합하여, 정교하게 설계된 노즐을 통하여 수평방향으로 토출시키도록 설계되어 있다[5,6]. 그러나 대형 정체수역, 또는 대형 호소에 설치되어야 한다는 단점이 있기에 적용하기 어렵다는 단점을 가지고 있다[7].
본 연구에서는 물순환장치의 이러한 단점을 해결하고자 다수의 Fin과 Body로 이루어진 표면 확산용 수중 방사형 임펠러를 개발하였다. 또한 비상시 Mode를 변경하여 넓은 수역에 약품을 혼합 확산이 가능하도록 설계하였다. 또한, 물순환장치의 최적화를 위해 수중 방사형 임펠러 가동시 유동흐름과 확산영역 등에 대한 정량적 해석이 필요하다. 특히, 기존의 물순환장치는 수중에서의 저층수와 상층수의 혼합을 기본 원리로 하여 수중에서만 유동을 하는 개념이나, 본 연구에 적용된 물순환장치는 수표면의 폭기와 수중 혼합을 동시에 일으킬 수 있는 임펠러 구조로 수중에서의 물 혼합과 수표면에서의 확산과 폭기를 위한 토출구의 유동을 함께 고려해야 하는 분석기법이 필요하다. 따라서, 기존의 수중의 유동만 고려하는 단일 phase 기법보다 다양한 층을 고려할 수 있는 Multi-phase를 이용한 기법을 적용한 것이 적합하다고 판단된다.
따라서, 본 연구에 적용된 물순환장치 수중 방사형 임펠러의 케이싱 형상, 날개의 각도, 개수에 따라 CFD를 활용하여 성능분석을 통해 최적의 Model 구조를 제안하고자 한다. 또한, 선정된 모형구조에 따른 유수면 해석이 가능한 VOF (volume of fraction)기법을 활용하여 정상상태, 비정상상태 조건에서의 물순환장치 수중 방사형 임펠러의 설계 최적화 인자를 도출하고자 한다.
2. 실험 방법 및 재료
2.1. 실험장치
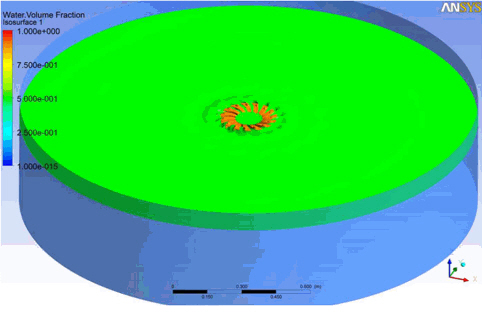
본 연구에 적용하고자 하는 물순환장치 수중 방사형 임펠러는 아래 Fig. 1과 같이 수중에서 상향수류를 생성하여 상·중·하부의 물을 혼합 후 수표면으로 표면분출하고 수면의 웨이브를 발생시키며 확산되는 특징이 있다. 또한, 물순환장치 수중 방사형 임펠러는 하천 및 댐 등 상수원과 수계에서 상시 물 순환으로 인한 수질개선과 비상시 약품 혼합·확산장치로서 두 가지 Mode를 가지고 있다.
물순환장치 수중 방사형 임펠러는 다수의 날개와 단일 케이싱으로 구성되어 있으며, Table 1에 나타낸 바와 같이 날개의 각도 및 크기, 유입부 및 토출부의 각도를 조절하여 수중 방사형 임펠러의 성능을 최적화할 수 있는 모델을 찾고자 하였다. Model II는 Model I의 날개 각도변경과 상부 직경의 확장형이며 회전방향으로 기운 날개와 토출부 직경의 확대로 물순환장치 하부로 유입된 유입수의 상승유속이 증가하도록 하였다. Model III은 보조 날개를 추가하여 수로(유도부)증가로 토출면적을 증가시켰으며 이로 인해 유입상승유속, 토출유속과 수직방향의 회전유속 증가로 인한 하부 영향이 증가하도록 하였다. 또한, 상부 토출부에서 분출된 유량의 재유입 방지를 위한 하부 유입구의 길이를 증가하도록 하였다. 특히 유속을 높이기 위해 분출각도를 회전방향으로 설계값의 최대치를 설정하였다.
2.2. CFD 지배방정식[8,9]
CFD해석기법의 기본 식은 직교 좌표계에 대해 질량, 운동량, 스칼라 보존방정식의 시간 평균된 형태는 다음과 같다.
이 방정식들은 검사체적에 걸쳐 적분되며, 체적적분(Volume integral)을 면적분(surface integral)으로 변환시키기 위해 가우스 발산이론(Gauss divergence theorem)이 적용된다. 검사체적은 시간에 따라 변하지 않으므로, 시간 미분항은 제한체적에 대한 적분식이 위치할 수 있고, 그 결과 적분식은 다음과 같다.
여기서 V와 S는 각각 적분체적과 면적을 나타낸다. 그리고 dnj는 제어체적을 구성하는 표면에서 바깥쪽으로 향하는 법선 벡터의 미소 직교좌표 성분이다. 면적적분은 유속(flux)에 대한 적분이며, 체적 적분은 제어체적 내의 축적항(accumulation), 또는 소스항(source)을 나타낸다.
검사체적이 변하는 경우에 대한 지배방정식의 변화를 아래에 나타내었다. 이 경우, 연속적인 방정식들을 수치적으로 해석하는 처음 단계는 이산함수를 사용하여 방정식을 근사화시키는 것이다. 위의 Fig. 2에 나타낸 독립된 메쉬에 대해 표면 유속은 연속적인 방정식을 이산화 형태로 변환하는 과정에서 각 적분점에 서로 다르게 표현되는데, ip로 표시되는 적분점은 삼차원의 유한 체적을 둘러싼 각 표면의 중심에 위치한다.
결과적으로, 적분 방정식은 다음과 같다.
여기서 V는 제어체적, 첨자 ip는 적분점, 합(summation)은 유한체적 내의 모든 적분점에 대한 합, nj는 표면을 통해 나가는 서로 다른 표면벡터, t는 시간간격을 나타낸다. 비록 second order scheme이 아래에 언급된 바와 같이 가능하지만, 이 방정식에는 first order backward Euler scheme이 사용되었다. 상첨자 0은 전 시간단계에서의 값을 의미한다. 제어 체적 면을 지나는 질량은 m i p ˙
2.3. Multi phase CFD 해석기법을 이용한 유동해석
본 연구에서는 물순환장치 수중 방사형 임펠러의 성능분석을 위해 자유표면을 포함하여 작동하는 특성을 정확하게 분석하기 위해 다상 유동(Multi phase) 해석 기법 중 VOF (Volume of Fraction)을 적용하였다. VOF 기법은 물과 공기의 두 가지의 상(phase)이 존재하는 체적비를 동시에 계산한 VOF결과를 이용하여 자유표면의 위치를 추적하는 매우 유용한 접근방법이다. 즉, 수위를 결정하고 물과 공기의 유속 및 압력 등의 특성을 예측하는 기법을 말한다[12,13]. 유체 체적 분율은 물이 점유하는 지점에서 VOF는 1이 되며, 공기의 VOF는 0으로 분류되고 0에서 1 사이의 값인 VOF 0.5는 자유표면으로 간주한다.
VOF 기법을 이용한 물순환장치 수중 방사형 임펠러의 유동해석은 정상상태와 비정상상태로 구분하여 수행하였다. 정상상태 조건에서는 자유표면에서의 VOF 결과를 통해 Model별 속도벡터와 유선흐름 분석을 하였고, 비정상상태 조건에서는 시간변화에 따른 속도, 온도 및 밀도의 공간적 변화를 지속적으로 계산하여 임펠러의 회전에 따라 자유표면에서의 흐름형태에 대해 분석하였다. 이를 위해 본 연구에서는 CFD 상용코드인 ANSYS CFX를 사용하였다. CFX는 고체해석 및 전자기장해석 등의 여러 다중물리 현상을 하나의 프로세스에서 연계하여 수행할 수 있는 프로그램으로 병렬계산이 가능하고 해석영역 및 메쉬의 수가 매우 방대한 유체기계 및 다상유동 해석에 가장 적합한 프로그램이다[10,11].
또한, 본 연구에 적용된 물순환장치 원리 및 특성을 반영하고 Multi phase기법을 활용하기 위해 임펠러와 임펠러 회전반경의 형상을 잘 나타낼 수 있도록 메쉬그리드 크기를 세밀하게 조정하여 유동해석을 정확하게 할 수 있도록 미세격자를 구성하였다. 특히, 이러한 미세격자 구성을 통한 공기와 물, 경계면, 그리고 임펠러로 인한 와류, 확산현상 등의 정밀한 유동흐름해석은 다양한 임펠러 구조조건에 있어 성능에 미치는 각 변수의 민감도 정보를 바탕으로 임펠러의 성능을 최적화할 수 있다.
메쉬생성은 3차원 캐드파일에서 추출한 step파일을 이용하였으며, ANSYS의 기본 메쉬생성 프로세스인 ANSYS mesh를 이용하였다. 또한, inflation 기능을 적용해 임펠러의 벽면의 경계층을 모사할 수 있다. 아래 Fig. 4에 나타낸 바와 같이 수중 방사형 임펠러의 메쉬형태는 Model별 구조조건에 따라 성능의 민감도가 클 것으로 예상되어 미세격자를 구축하여 Multi phase(공기, 물, 경계면)조건과 임펠러에 의한 와류 등 정밀한 유동흐름분석을 할 수 있는 구조로 구축하였다. 특히, 물순환장치의 회전을 고려하여 장치를 포함한 내부의 rotating domain과 분석을 위한 원형메쉬를 포함하는 stationary domain 두 영역으로 나누어 구성하였으며, 메쉬그리드 개수는 임펠러 Model별로 상이하며 총 3,600,000-4,370,000개로 구축하였다.
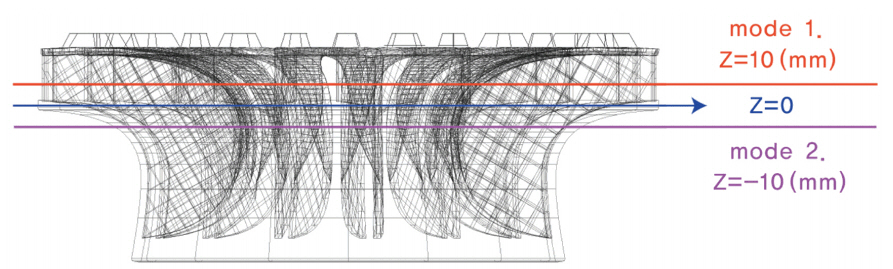
물순환장치 수중 방사형 임펠러의 Mode 변화에 따른 해석 수면 위치를 Fig. 5에 나타냈다. 토출부의 최저높이를 Z = 0 (mm)로 설정하고 Mode 1에서는 Z = 0 (mm)로부터 상부로 10 mm 높인 위치를 수면위치로 하고 Mode 2에서는 Z = 0 (mm)로부터 하부로 10 mm 내린 위치를 수면위치로 설정하였다.
3. 결과 및 고찰
3.1. 수중 방사형 임펠러의 속도벡터 및 VOF 분석
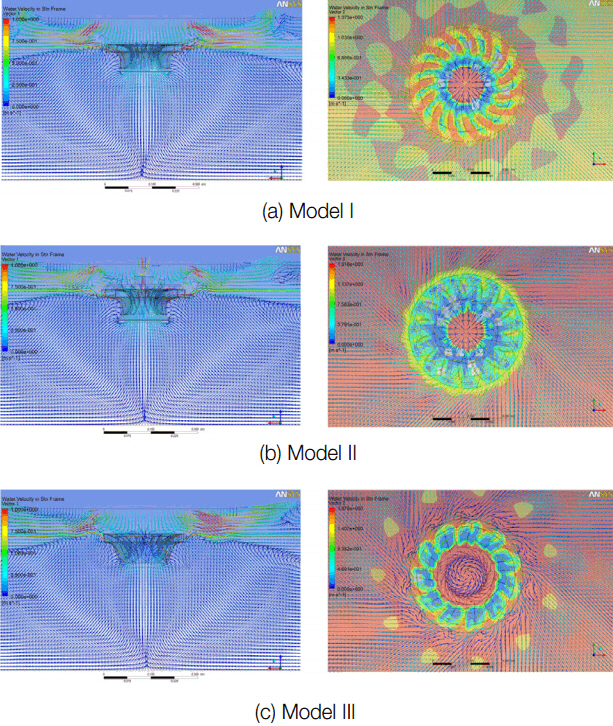
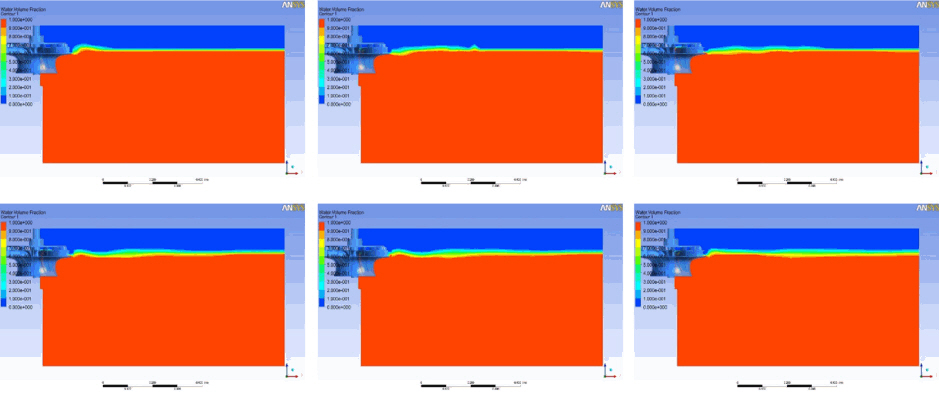
아래 Fig. 6은 정면과 평면에서 모델별 속도벡터와 VOF결과 값을 나타냈다. VOF 자유표면에서 360° 전체의 평균값이 아닌 임의 각도의 값으로 날개의 위상에 따라 달라지고 윤곽선은 0-1구간을 파란색에서부터 빨간색으로 표현하였으며, 속도벡터의 크기는 모델에 따라 범례에 표시하였다. Model I-III 모두 하부에서 생성된 압력으로 인해 상승수류를 생성되어 유입부로 유입 후 회전에 의해 원심력을 얻어 반경방향으로 빠르게 분출되는 유동이 특성이다. 자유표면으로 분출된 유동의 지속적인 유입으로 인해 분출된 제트유동의 폭이 하류로 진행될수록 점점 선형적으로 증가하고 있으며, 하부의 유동이 회전축 방향으로 모인 후 물순환장치의 유입구 쪽으로 상승하는 현상을 보인다.
Model I은 벡터에서 토출구인 Z = 0에서 수직 분출각도는 6.83°로 토출구에서 약간 낮은 상태에서 평행에 가까운 각도로 분출한다. 회전축에서 속도벡터는 반경방향의 성분만 포함하고 있으며 날개 내부에서 가속되어 날개 끝단에서 최대속도 1.37 m/s이며 토출면 평균속도는 1.07 m/s 값을 보인다. 또한, Model II는 자유표면의 속도벡터에서 토출구인 Z = 0에서 수직 분출각도는 7.55°로 나타났다. 평면도 속도벡터와 VOF 결과 회전축 부근의 유동은 Model I과 큰 차이가 없으나 날개 끝단에서 원주방향 속도성분의 증가로 인해 분출각이 변화하였으며 최대속도는 1.52 m/s이고 토출면 평균속도는 1.32 m/s로 나타났다. VOF 결과값을 통해 회전축에서 날개방향으로 진행되면서 점진적으로 수위가 증가하는 것을 확인할 수 있다. [Table 3]
Model III은 자유표면의 속도벡터 결과 분출각도는 7.76°로 Model I과 Model II에 비해 수직영향범위가 넓으며 이는 분출로 인한 직접적인 영향범위의 증가로 Model I과 Model II에 비해 넓고 강한 표면웨이브를 형성한다. 회전축 부근에서는 강한 와동이 발생했으며 날개의 끝단이 후향곡선(backward-curved)인 Model I과 Model II와 다르게 Model III은 미세하게 전향곡선(forward-curved)으로 설계되어 반경 방향 성분에 비해 원주방향 속도가 크며 VOF 값이 상대적으로 높게 분포하고 있다. 토출면 최대속도는 1.88 m/s이고 평균속도는 1.50 m/s로 가장 높게 나타났으며 동일한 회전수에서 교반이 유리하나 필요 소요동력은 증가할 것으로 판단된다.
3.2. 임펠러 Model별 유선(streamlines)해석
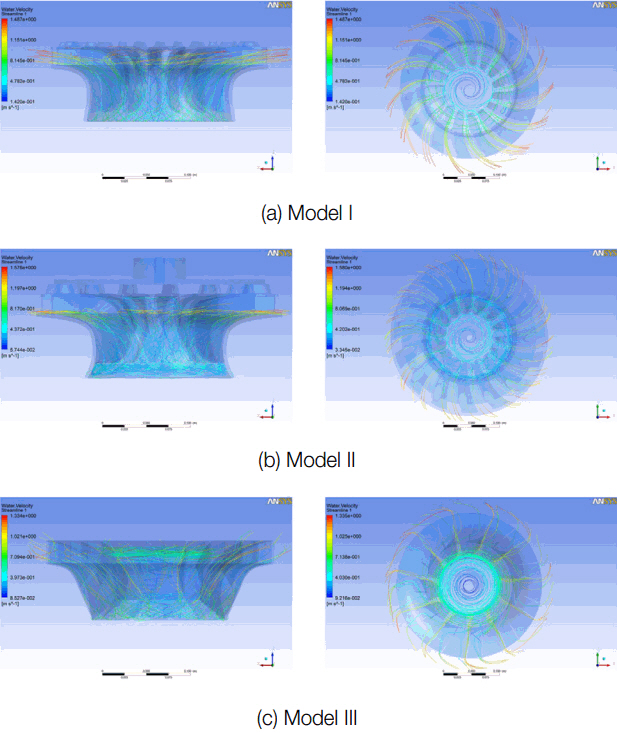
다음 Fig. 7은 물순환장치를 포함한 rotating domain의 좌표를 기준으로 도출된 모델별 유선(streamlines)의 정면도와 평면도의 결과이다. 유선해석을 통한 상부 유출각도와 평면 유출방향 및 유선의 tangle 정도를 알 수 있으며 분출각도는 토출유동이 수표면에 탄착되는 거리를 나타낸다.
Model I은 평면과 정면의 유선의 방향은 유출각도와 동일한 흐름을 보이며 유선의 흐름은 꺾이는 현상이 적어 부드럽게 진행하며 유선이 토출구인 Z = 0에서 상부로 4.13° 분출 범위를 나타내었다. Model II는 평면과 정면의 유선의 각도나 흐름이 Model I과 유사한 결과를 나타내었다. 날개끝부분에서 유출되는 유동에 비해 회전속도가 다소 빨라 유선이 뒷부분으로 꺾이는 현상을 보인다. 유선이 토출구인 Z = 0에서 1.43°의 분출범위로 토출구에서 약간 높거나 평행한 상태로 진행되어 수표면의 탄착거리가 상대적 짧을 것으로 예상된다. 또한, Model III은 토출구에서 날개의 회전속도가 상대적으로 빨라 유선의 꺾임현상이 뚜렷하게 나타나고 회전축에서 지속적인 와동을 보이며 Fig. 7에서도 확인할 수 있다. 유선이 토출구인 Z = 0에서 9.67°의 분출범위를 나타내며 Model I과 Model II에 비해 상대적으로 높게 분출하는 것을 알 수 있다. 따라서, Model III는 타 모델에 비해 유속과 수표면 탄착거리가 상대적 높을 것으로 판단된다. 이는 Fin의 각도로 인한 것으로 Model III의 경우 유속을 높이기 위한 분출각도를 회전방향으로 설계 값의 최대치를 설정한 결과로 판단된다.
3.3. 수중방사형 임펠러의 유동 및 속도분포
물순환특성을 정량적으로 계산하기 위해서는 비정상상태의 유동해석이 필요하다. 비정상상태의 유동해석은 시간의 변화에 따른 속도 및 온도, 밀도의 공간적인 변화를 지속적으로 계산하는 방법이며 정상유동해석과 달리 회전에 따라 자유표면이 주기적으로 파동을 생성하는 것을 관찰할 수 있으며 실제 실험에서 관찰할 수 있는 유동특성과 유사한 형태를 보인다.
아래 Fig. 8은 Model II의 물순환장치 수중 방사형 임펠러의 운동에 따른 자유표면의 거동을 0.085초 간격으로 나타낸 결과이다. 물순환장치 가동 후 날개 전후의 자유표면 차이로 인한 파동을 볼 수 있으며 혼합 및 확산과정에서 우호적인 영향을 미칠 것으로 분석된다. 생성된 파동은 점차 하류로 진행하며 최종적으로 벽면까지 진행된다.
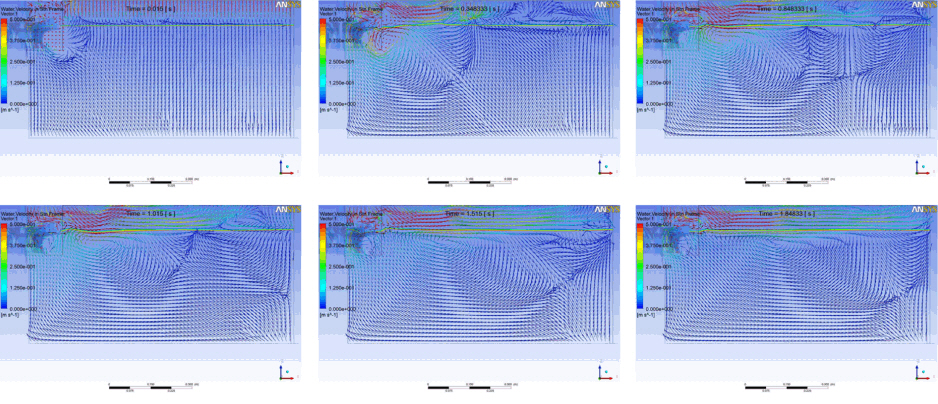
아래 Fig. 9는 Model II의 물순환장치 수중 방사형 임펠러의 가동에 따른 속도분포와 자유표면의 운동을 동시에 나타낸 결과이며 0.17초 간격으로 해석하였다. 가동 초기에 토출구 쪽에서 시계방향으로 강한 와동이 발생되며 시간이 진행됨에 따라 하부로 이동하며 물순환장치의 영향권이 증가하는 것을 알 수 있다. 속도분포는 날개의 회전에 의해 중앙에서 외부로 상하로 진동하며 진행되었다. 속도벡터의 크기를 동일하게 설정하여 속도벡터의 방향이 하류구간에서는 급격하게 변화하는 것으로 관찰되지만, 실제로는 속도벡터의 크기가 매우 작기 때문에 실제보다 과장되게 표현된 것으로 판단된다.
3.4. VOF해석에 따른 운전인자 비교
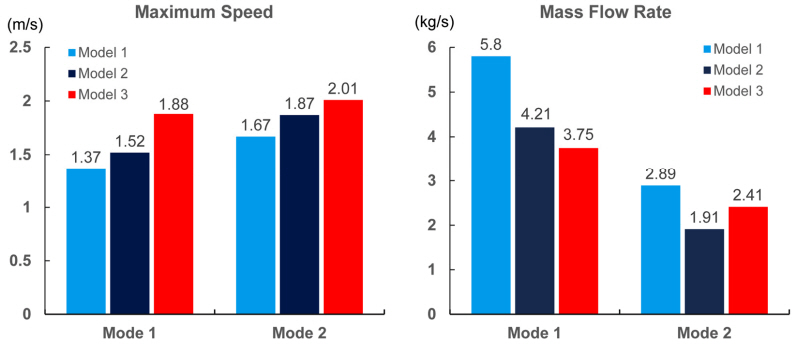
아래 Fig. 10~12는 물순환장치 수중 방사형 임펠러 Model별 VOF 해석으로 최대속도 및 유량, 축동력을 분석한 결과이다. 최대 토출속도는 동일 rpm을 유지할 때 Model III에서 2.01 m/s로 높게 나타났으며, 유량은 Model I에서 질량기준으로 5.80 kg/s로 가장 높게 나타났다.
또한, 축동력은 Model III, I, II 순서로 나타났으며, 동일한 rpm에서 축동력 대비 유량(m/s per w) 및 유속(kg/s per w)에 대한 효율은 Model II이 높게 나타났다. 따라서, 수중 방사형 임펠러의 설계인자인 Fin 구조 조건에 따라 토출각도 및 흡입각도를 다르게 한 결과, 토출유속 및 유량변화를 결정할 수 있어 향후 현장실험을 위해 제작되는 임펠러의 설계 최적화 인자로서 활용할 수 있을 것으로 판단된다. (Table 4)
4. 결 론
본 연구에서는 물순환장치의 수중 방사형 임펠러의 성능을 높이고자 날개의 각도 및 크기, 유입부 및 토출부의 각도를 조절하여 임펠러의 최적화할 수 있는 모델을 찾고자 하였으며, 물순환장치의 운전특성을 반영할 수 있는 Multi phase CFD해석기법을 적용하여 VOF 및 유동해석결과 다음과 같은 결론을 얻었다.
1) 수중 방사형 임펠러의 구조조건에 따라 성능효율에 민감도를 보일 것으로 예상되어 물순환장치를 포함한 내부의 rotating domain과 원형메쉬를 포함하는 stationary domain영역으로 나누어 총 3,600,000~4,370,000개의 메쉬를 구축하였다.
2) 수중 방사형 임펠러의 운전특성을 반영한 Multi-phase CFD해석기법을 적용하여 VOF 해석을 한 결과, Model III는 수직범위로 가장 넓은 분사 범위를 나타냈으며, 이는 토출로 인해 직접적인 영향범위의 증가로 다른 Model에 비해 넓고 강한 표면 웨이브를 형성하였다.
3) Model I, II는 단순한 유선(streamlines)을 형성한 반면 Model III은 복잡한 유선을 형성하였다. 유량ㅊ에 대한 결과 값은 유선형성이 단순한 Model I, II에서 높게 나타났으며, 유속에 대한 결과값은 Model III에서 높게 나타났다. 이는 Fin의 각도로 인한 것으로 Model III의 경우 유속을 높이기 위한 분출각도를 회전방향으로 설계 값의 최대치를 설정한 결과로 판단된다.
4) Model II는 물순환장치 가동 후 날개 전후의 자유표면 차이로 인한 파동을 볼 수 있었고, 가동 초기에 토출구쪽에서 시계방향으로 강향 와동이 발생되며 시간이 지남에 따라 하부로 이동하여 물순환장치의 영향권이 확산하는 것을 볼 수 있었다.
5) 동일한 rpm에서 각 Mode I의 결과를 분석한 결과 축동력 대비 유량 및 유속에 대한 효율은 Model II가 높게 나타났으나, 최대 토출속도는 동일 rpm을 유지할 때 Model III에서 2.01 m/s 가장 높게 나타났으며, 유량은 Model I에서 질량기준으로 5.80 kg/s 가장 높게 나타났다.