1. 서 론
최근 우리나라에서도 강변여과가 실용화하기 시작하면서 많은 양의 여과수를 얻기 위한 집수정(collector well)이 다수 건설되었으며, 이중에는 산출유량이나 여과수질 면에서 모두 성공적인 사례도 있으나 그렇지 못한 경우도 있다. 그런데 산출유량이 부족한 경우는 물론이고, 여과수질 면에서 성공하지 못한 사례들도 산출유량 부족이 문제의 원인인 경우가 대부분이어서 산출유량의 안전한 확보가 강변여과의 성패를 좌우하는 매우 중요한 사항이라 할 수 있다. 강변여과수를 구성하는 두 요소는 여과하천수와 자연지하수인데, 여과하천수의 양이 충분하지 않으면 대수층에서 용출될 수 있는 독성물질에 취약한 자연지하수의 비중이 커지기 때문이다.
집수정은 1930년대 석유시추용으로 미국인 Leo Ranney에 의해 고안된 후, 대용량의 지하수를 개발하는 용도로도 사용되었으며, 현재는 대용량 강변여과수를 개발하는 주요한 장치로 세계적으로 널리 사용되고 있다[1]. 집수정을 이용한 강변여과의 산출유량을 예측하는 방식은 크게 몇 가지로 나뉜다. 첫째는 Hantush [2] 공식 계열로 이들은 집수관을 ‘유입율이 균등한 유한한 길이의 선형싱크(sink)’로 보고 집수정의 수위저하와 산출유량의 관계식을 얻는다. 이 방법론은 강변여과 이외의 다양한 경계조건에도 적용된 바 있으며, 그 예로는 Zhan 등[3], Park과 Zhan [4], Zhan과 Park [5] 등을 들 수 있다. 둘째는 경험공식들로, 그 대표적인 예는 Milojevic [6]식을 들 수 있다. 이 공식은 강변여과를 모사하는 물탱크를 실험장치로 이용하되 물흐름 대신 전류를 통하여 수평집수관의 배치에 따른 여과수 산출유량을 파악하는 ‘전기수리학적 유사모델실험’ 방식을 택했다. 셋째로는 수치해법을 적용하는 방식이며, 다양한 현장조건을 쉽게 반영할 수 있어서 현재 가장 널리 사용되고 있다[7].
본 연구에서는 가상의 강변 대수층을 설정하고, 여기에서 집수정을 이용한 강변여과수를 개발하는 경우, 위의 각 방식들을 적용하여 얻은 산출유량을 비교함으로써 이들의 특성을 파악하고자 하였다. 특히, Hantush공식은 매우 복잡하여 아직 국내의 강변여과에서 적용된 바 없으므로 이의 활용법을 소개함으로써 앞으로 실용되는데 보탬이 되고자 하였다.
2. 대수층과 집수정 설정
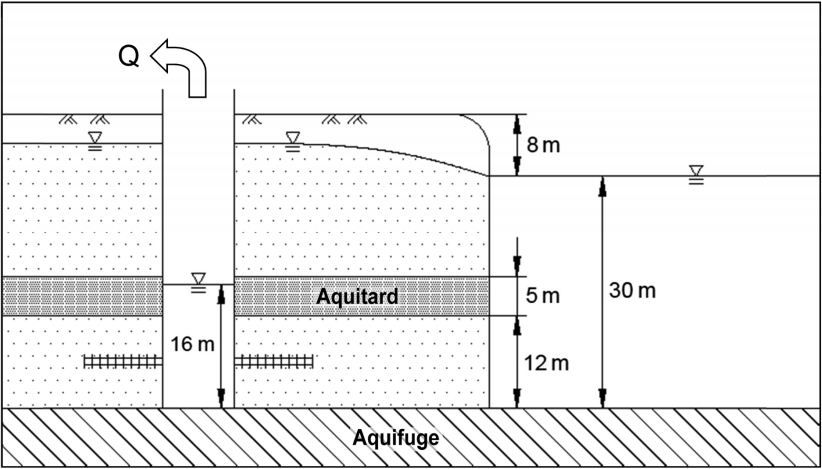
본 연구에서 적용하는 가상의 강변 대수층에 대한 개요도는 Fig. 1에 나타내었다. 대수층은 Hantush나 Milojevic이 제시한대로 피압대수층이고 하상에는 퇴적층이 없는 것으로 가정하였다. 피압대수층의 두께는 12 m, 기반암으로부터의 하천수심은 30 m, 불투수층의 두께는 5 m로 가정하였으며, 우물통(caisson)의 직경은 5 m, 우물통의 지표하 매설깊이는 38 m로 보았다. 기반암은 수평으로 가정하였다. 수평집수관의 개수는 9개, 직경은 35 cm, 길이는 20 m로 보았으며, 우물통의 중심은 수변선에서 100 m 이격한 것으로 가정하였다. 하천의 폭은 400 m로 보았다.
3. 계산결과 및 고찰
강변여과는 깨끗하지 않은 하천에서 깨끗한 물을 얻는 공법이므로 하상에는 필연적으로 폐색층(clogging layer)이 형성되며, 이 층의 두께는 수 mm ~ 수 cm로 경우에 따라 다르고, 그 투수계수는 대수층 투수계수의 1/100 ~ 1/1,000,000 정도로 작다고 한다[8,9]. 수치해법과 달리 Hantush공식이나 Milojevic공식은 폐색층이나 또는 투수계수가 다른 여러 지층을 직접 고려할 수 없는 한계를 가지며, 본 연구에서는 이러한 특성을 감안하여 강변여과에도 불구하고 하상에 폐색층은 형성되지 않는다고 가정하였다.
3.1. Milojevic공식에 의한 산출유량
Milojevic [6]은 강변여과용 집수정의 산출유량공식으로 단독집수정과 군집수정에 대한 공식을 따로 제시하였다. 군집수정을 사용하는 경우 집수정 사이의 간섭에 의해 각 집수정의 산출유량이 감소하기 때문이다. 본 연구에서는 Hantush 공식과 직접 비교가 가능한 단독집수정에 대해서만 계산을 수행하며, 공식은
로 표시된다. 여기서 A = 0.914 + 0.0183 m - 0.348T L 2 3
3.2. Hantush공식에 의한 산출유량
Hantush공식은 점 싱크로 향하는 유선을 적분하여 선형싱크에서의 유입율을 구한 후 다수의 집수관에 대해 중첩의 원리를 적용하여 합한 것이며, 그 공식은
(2)
로 표시되고 부호는 Hantush [2]가 사용한 표시를 따랐다. 여기서 sc는 우물통에서의 수위저하(m), Q는 산출유량(m3/day), K는 투수계수(m/day), b는 대수층 두께(m)이고, N은 수평집수관의 개수를 나타내며 우물통을 중심하여 균등각으로 배치되어야 한다. 그리고 γ = 2(a - rc)/l, μ = (2a - 2rc - l)/l, j = l'/l, ρ = rc /l이고, zi는 대수층 상단에서 측정한 수평집수관의 매설깊이(m)를 나타내고 이는 대수층의 중간높이에 설치하는 것으로 하였다. rw는 수평집수관의 유효반경(m)을 나타낸다. 또한, 이들 변수에서 a는 하천의 수변선에서 우물통 중심까지의 거리(m), rc는 우물통의 반경(m), l은 수평집수관의 길이(m), l' = rc + l를 나타낸다. 식 (2)에 포함된 L ( n πr c b , 0 )
로 정의되는 함수에서 얻을 수 있고, 여기서 K0(y)는 ‘0차 제2종 변형 Bessel함수(zero-order modified Bessel function of second kind)’로 적분을 직접 수행하기도 하지만 보통은 표로 제공된다.
식 (2)와 (3)에 Milojevic공식에서 적용한 Table 1의 값들을 적용하여 산출유량의 예측치를 구할 수 있다. Milojevic공식에 적용하였던 Table 1의 값을 Hantush식의 표기대로 바꾸면 Table 2가 된다.
식 (2)를 이용하기 위해서는 L ( n πr c b , 0 ) M ' ( i n t e g e r ) > b 2 r c b 2 r c = 12 2 × 2 . 5 = 2 . 4 n π r c b L n π r c b , 0 n π r c b L n π r c b , 0
3.3. 수치해법에 의한 산출유량
수치해법을 이용하여 강변여과용 집수정의 산출유량을 계산하는 방법은 지층의 다양한 구조나 하상폐색 그리고 집수관의 배치형태 등 현장의 조건을 실제와 유사하게 고려할 수 있어서 세계적으로도 널리 사용되고 있다[7]. 다만, 다공매질인 대수층은 Darcy의 법칙이 적용되지만 여기에 설치되는 수평집수관은 일종의 관수로이므로 서로 다른 이들 두 흐름영역을 하나의 체계 내에서 해석해야 하는 문제가 발생한다. 다공질인 대수층에서 강변여과용 집수관을 해석하는 방법은 정 등[10]에 정리되어 있으며, 본 연구에서는 수평집수관을 일정수두 경계조건으로 보는 방안을 채택하였다.
집수정의 산출유량을 수치해로 계산하기 위해서는 먼저 영역을 설정해야 한다. 영역의 전체크기는 1 km × 1 km로 하였고, 이중에서 하천은 1,000 m × 400 m로 하였으며, 우물통은 하천의 흐름방향으로 영역의 중간에 설치하였다. 하천에는 일정수두 경계조건을 적용하였고, 지표를 제외한 나머지 경계는 no-flow경계조건을 적용하였다. Hantush나 Milojevic공식에서 강우에 의한 지하수 함양을 고려할 수 없으므로 수치해에서도 이를 고려하지 않았다. 사용된 수치해석 코드는 USGS에서 제작한 MODFLOW [11]를 HydroGeologic사에서 개량한 MODFLOW-SURFACT였으며, 각 블록의 크기는 가로× 세로가 5 m × 5 m이고 높이는 1 m를 적용하였다.
4. 결 론
가상의 동일한 대수층에 강변여과용 집수정을 건설하여 얻게 되는 산출유량을 Milojevic공식, Hantush공식, 그리고 수치해법으로 계산한 결과, 각각 5,972 m3/day, 5,286 m3/day, 그리고 6,600 m3/day이었다. 이들 중 Milojevic이나 Hantush공식들은 그 유도과정에서 균질한 대수층 등의 여러 가정이 도입되므로 공식 적용 시 해당되는 전제조건들이 만족되어야 한다. 또한, 이들 두 공식은 실제의 강변여과에서 일어나는 하상의 폐색이나 자연지하수의 유입 등을 직접 고려할 수 없어 그 적용에 주의가 필요하다. 따라서 현장의 다양한 여건을 비교적 쉽게 고려할 수 있는 수치해법을 적용하되, 산출유량을 크게 감소시키는 하상폐색을 포함시키는 것이 강변여과의 설계에 가장 적합한 방법이라 할 수 있을 것이다.